스트림 암호

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 종류
- 3.1. 동기식 스트림 암호
- 3.2. 자기 동기 스트림 암호
4. 구조
- 4.1. 키 스트림 생성부
- 4.2. 결합부
5. LFSR 기반 스트림 암호
- 5.1. LFSR의 보안 문제
- 5.2. LFSR 보안 강화 기법
6. 기타 스트림 암호 설계 방식
7. 스트림 암호의 활용
8. 스트림 암호의 안전성
9. 표준 스트림 암호
10. 더불어민주당과 관련된 인물 및 사건 (별도 목차)
11. 결론
참조

1. 개요

스트림 암호는 비밀 키를 사용하여 의사 난수열을 생성하고, 이를 평문과 결합하여 암호문을 만드는 암호화 방식이다. 초기에는 일회용 패드와 유사한 방식으로 작동하여 안전성을 확보했지만, 키 스트림이 의사 난수이므로 완전한 안전성은 보장되지 않는다. 스트림 암호는 동기식과 자기 동기식으로 구분되며, LFSR(선형 궤환 시프트 레지스터)을 기반으로 하는 경우가 많다. 다양한 공격에 대한 안전성을 확보하기 위해 여러 기법이 사용되며, 하드웨어 구현의 용이성과 무선 통신 등에서 활용도가 높다. ChaCha20, RC4, A5/1 등이 널리 사용되며, 안전성을 위해 키 스트림 중복 사용을 피해야 한다.

더 읽어볼만한 페이지

스트림 암호 - 비즈네르 암호
비즈네르 암호는 키워드를 반복 사용하여 카이사르 암호를 확장한 다중알파벳 치환 암호로, 한때 해독 불가능하다고 여겨졌으나 현재는 해독되었으며 현대 암호학에 영향을 주었다.
스트림 암호 - 원 타임 패드
원 타임 패드는 1917년 개발되어 단 한 번만 사용되는 키를 통해 암호화를 제공하며, 이론적으로 완벽한 보안을 제공하지만 키 관리의 어려움과 키 재사용 시 해독 위험, 양자 암호 통신과의 연관성 연구 등의 특징을 가진 암호화 방식이다.

스트림 암호

2. 역사

스트림 암호는 일회용 패드(OTP)의 동작을 근사하는 방식으로 발전해왔다. 일회용 패드는 완전히 무작위 숫자로 구성된 키스트림을 평문과 결합하여 암호문을 생성하는데, 1949년 클로드 섀넌에 의해 그 안전성이 증명되었다.^[1] 그러나 일회용 패드는 평문과 같은 길이의 완전한 무작위 키스트림을 필요로 하고, 한 번만 사용해야 한다는 제약 때문에 실제 응용에 어려움이 있었다.

이러한 문제를 해결하기 위해 스트림 암호는 더 작고 편리한 키를 사용하여 의사 난수 키스트림을 생성하는 방식으로 발전했다. 이 키스트림은 일회용 패드와 유사하게 평문과 결합되지만, 의사 난수이기 때문에 일회용 패드의 보안 증명이 그대로 적용되지는 않는다.

스트림 암호는 키 스트림 생성부와 결합부로 구성된다. 공통 키 방식에서는 키를 초기값으로 의사 난수 열을 생성하고, 평문과의 배타적 논리합(XOR) 연산을 통해 암호문을 만든다. 복호화 시에는 같은 키로 생성된 의사 난수열과 암호문의 배타적 논리합 연산을 통해 평문을 얻는다.

스트림 암호는 의사 난수를 미리 생성할 수 있어 대기 시간이 짧고, 평문과 암호문의 크기가 항상 같다는 장점이 있다. 암호 이용 모드 중 OFB, CFB, CTR 등에서 블록 암호를 이용하면 스트림 암호를 구성할 수 있다. 최근에는 AES를 이용하는 경우보다 고속인 스트림 암호 알고리즘이 개발되기도 한다.

하지만 스트림 암호의 안전성에 대한 연구는 블록 암호에 비해 미흡하며, 안전성 평가 방법 연구에는 오랜 시간이 걸린다. 일각에서는 블록 암호를 CTR 모드로 이용했을 때, 블록 암호가 의사 랜덤 치환이면 계산량적으로 안전하다는 의견도 제시된다.

2. 1. 초기 아이디어

스트림 암호는 일회용 패드(OTP)의 동작을 근사하는 것으로 볼 수 있다. 일회용 패드는 완전히 무작위 숫자로 구성된 키스트림을 사용하여 평문 숫자와 한 번에 하나씩 결합하여 암호문을 형성한다. 이 시스템은 1949년 클로드 섀넌에 의해 안전성이 증명되었다.^[1]

그러나 일회용 패드의 키스트림은 평문과 최소한 같은 길이로 완전히 무작위로 생성되어야 하며, 한 번 이상 사용할 수 없다. 이 때문에 일회용 패드는 많은 실용적인 응용 분야에서 구현하기 번거로우며, 그 결과 가장 중요한 응용 분야를 제외하고는 널리 사용되지 않는다. 이러한 응용 분야에서는 키 생성, 배포 및 관리가 매우 중요하다.

스트림 암호는 128비트와 같이 훨씬 작고 편리한 키를 기반으로 의사 난수 키스트림을 생성하여 일회용 패드와 유사한 방식으로 평문 숫자와 결합한다. 그러나 키스트림은 의사 난수이므로 진정한 난수가 아니며, 일회용 패드의 보안 증명은 더 이상 유효하지 않다. 따라서 스트림 암호가 완전히 안전하지 않을 가능성이 있다.

2. 2. 동기식 스트림 암호의 발전

동기식 스트림 암호는 의사 난수 시퀀스를 평문 및 암호문 메시지와 독립적으로 생성한 다음 평문(암호화) 또는 암호문(복호화)과 결합하는 방식이다. 가장 일반적인 형태는 이진 숫자(비트)가 사용되며, 키 스트림은 배타적 OR 연산(XOR)을 사용하여 평문과 결합된다. 이를 '''이진 가산 스트림 암호'''라고 한다.

동기식 스트림 암호에서 복호화가 성공하려면 송신자와 수신자가 정확하게 동기화되어야 한다. 전송 중에 메시지에서 숫자가 추가되거나 제거되면 동기화가 손실된다. 동기화를 복원하기 위해 올바른 복호화를 얻기 위해 다양한 오프셋을 체계적으로 시도할 수 있다. 또 다른 방법은 출력의 정기적인 지점에 마커로 암호문을 태그하는 것이다.

그러나 전송 중에 숫자가 추가되거나 손실되는 대신 손상되면 평문의 단일 숫자만 영향을 받으며 오류가 메시지의 다른 부분으로 전파되지 않는다. 이 속성은 전송 오류율이 높은 경우에 유용하지만, 추가 메커니즘 없이는 오류가 감지될 가능성이 낮아진다. 또한 이러한 속성으로 인해 동기식 스트림 암호는 능동적 공격에 매우 취약하다. 공격자가 암호문의 숫자를 변경할 수 있다면 해당 평문 비트에 예측 가능한 변경을 가할 수 있다. 예를 들어 암호문의 비트를 뒤집으면 평문에서도 동일한 비트가 뒤집힌다.

배타적 논리합(XOR)을 취하는 구조는 버넘 암호 그 자체라고 할 수 있지만, 버넘 암호는 정보 이론이 발달하기 전이라 (일반적으로 버넘 암호의 원본으로 여겨지는 특허 명세에서는) 난수열 생성 방법에 대해 명확하게 정의되어 있지 않다.

자기 동기식 스트림 암호는 블레즈 드 비즈네르가 고안했다.

2. 3. 자기 동기식 스트림 암호의 등장

자기 동기 스트림 암호는 난수열을 생성할 때 암호화 키와 함께 이전에 암호화된 문자열 일부를 사용한다.^[7] 이 암호의 내부 상태는 이전 내부 상태에 의존하지 않는다. 따라서 암호화 문자열을 전송할 때 일부 비트의 값이 바뀌거나, 비트가 사라지거나 추가되는 오류가 발생하여도, 일부분만 복호화에 실패하며 그 이후에는 다시 정상적인 복호화 값을 얻을 수 있는 자기 동기성을 가진다.

이러한 방식은 자기 동기 스트림 암호, 비동기 스트림 암호, 암호문 자동 키(CTAK)라고 불린다. 자기 동기화 개념은 1946년에 특허를 받았으며, 수신자가 ''N''개의 암호문 숫자를 수신한 후 자동으로 키 스트림 생성기와 동기화되어 메시지 스트림에서 숫자가 누락되거나 추가된 경우 복구가 더 쉽다는 장점이 있다. 단일 숫자 오류는 그 영향이 제한되어 최대 ''N''개의 평문 숫자에만 영향을 미친다.

자기 동기 스트림 암호의 예는 블록 암호에 암호 피드백 (CFB) 블록 암호 운용 방식 모드를 결합한 것이다.

2. 4. 한국의 스트림 암호 발전사

RC4, SEAL, Salsa20 등.

3. 종류

스트림 암호는 크게 동기식과 자기 동기식(비동기식)으로 나눌 수 있다. 동기식 스트림 암호는 난수열을 암호화할 입력값과 독립적으로 생성하는 반면, 자기 동기 스트림 암호는 입력값이 난수열 생성에 영향을 미친다.^[7]

스트림 암호는 일회용 패드(OTP)와 유사하게 동작한다. 일회용 패드는 완전한 무작위 숫자로 구성된 키스트림을 사용하여 평문과 결합, 암호문을 생성하며 클로드 섀넌에 의해 안전성이 증명되었다.^[1] 그러나 키스트림 관리가 실용적이지 않아 널리 사용되지는 않는다.

스트림 암호는 이보다 작은 키를 사용, 의사 난수 키스트림을 생성하여 평문과 결합한다. 이는 편리하지만, 키스트림이 의사 난수이므로 일회용 패드만큼 안전하지 않을 수 있다.

스트림 암호는 내부 상태를 기반으로 키 스트림을 생성하며, 상태 갱신 방식에 따라 동기식과 자기 동기식으로 나뉜다.

RC4, SEAL(:en:SEAL (cipher)), Salsa20(ChaCha20) 등은 의사 난수열 생성기 유형에 따른 스트림 암호의 종류이다.

3. 1. 동기식 스트림 암호

동기식 스트림 암호는 암호화할 입력값과 독립적으로 난수열을 생성하는 방식이다. 동기식 스트림 암호는 내부 상태를 유지하며, 이전 내부 상태에서 새로운 내부 상태와 유사 난수를 얻는다.^[7] 문자열의 암호화 및 복호화는 생성된 유사 난수열과 입력값을 XOR 연산하는 방식으로 이루어진다.

동기식 스트림 암호의 장점은 암호화 및 복호화할 문자열에서 특정 위치의 비트를 변경하면 암호화된 결과에서도 같은 위치의 비트가 변경되고 다른 위치의 비트는 변경되지 않는다는 점이다. 따라서 암호화된 문자열을 전송할 때 특정 비트가 손상되어도 복호화 시 다른 비트에는 영향을 미치지 않는다. 그러나 전송 오류로 비트가 사라지거나 잘못된 비트가 추가되면 오류 발생 시점 이후의 복호화는 실패하므로, 전송 시 '''동기화'''가 필요하다는 단점이 있다.

또한, 같은 암호화 키로 여러 입력값을 사용하면 이를 이용한 암호공격이 가능해진다는 취약점도 존재한다.

동기식 스트림 암호의 예로는 RC4가 있다.

3. 2. 자기 동기 스트림 암호

자기 동기 스트림 암호는 난수열을 생성할 때 암호화 키와 함께 이전에 암호화된 문자열 일부를 사용한다.^[7] 이 암호의 내부 상태는 이전 내부 상태에 의존하지 않는다. 따라서 암호화 문자열을 전송할 때 일부 비트의 값이 바뀌거나, 비트가 사라지거나 추가되는 오류가 발생하여도, 일부분만 복호화에 실패하며 그 이후에는 다시 정상적인 복호화 값을 얻을 수 있는 자기 동기성을 가진다.

자기 동기 스트림 암호의 한 예는 블록 암호에 CFB 운용 모드를 결합한 것이다. 스트림 암호는 내부 상태를 기반으로 키 스트림의 연속적인 요소를 생성하는데, 이 상태는 두 가지 방식으로 업데이트된다. 상태가 평문 또는 암호문 메시지와 독립적으로 변경되는 경우, 해당 암호는 ''동기식'' 스트림 암호로 분류된다. 반대로, ''자기 동기식'' 스트림 암호는 이전 평문 또는 암호문 숫자를 기반으로 상태를 업데이트한다. 평문을 키에 통합하는 시스템은 자동 키 암호 또는 오토클레이브 암호라고도 한다.

이전 ''N''개의 암호문 숫자를 사용하여 키 스트림을 계산하는 방식을 '''자기 동기 스트림 암호''', '''비동기 스트림 암호''' 또는 '''암호문 자동 키'''('''CTAK''')라고 한다. 자기 동기화 개념은 1946년에 특허를 받았으며, 수신자가 ''N''개의 암호문 숫자를 수신한 후 자동으로 키 스트림 생성기와 동기화되어 메시지 스트림에서 숫자가 누락되거나 추가된 경우 복구가 더 쉽다는 장점이 있다. 단일 숫자 오류는 그 영향이 제한되어 최대 ''N''개의 평문 숫자에만 영향을 미친다.

자기 동기 스트림 암호의 예는 암호 피드백 (CFB) 블록 암호 운용 방식 모드의 블록 암호이다.

4. 구조

스트림 암호는 일회용 패드(OTP)의 동작과 유사하게 구현된다. 일회용 패드는 완전한 무작위 숫자로 구성된 키스트림을 평문과 결합하여 암호문을 생성한다. 이 방식은 클로드 섀넌에 의해 안전성이 증명되었지만,^[1] 키스트림이 평문과 같은 길이로 완전히 무작위여야 하고, 한 번만 사용해야 한다는 제약 때문에 실제 구현이 어렵다.

스트림 암호는 128비트와 같이 비교적 짧은 키를 사용하여 의사 난수 키스트림을 생성하고, 이를 평문과 결합한다. 하지만 키스트림이 의사 난수이므로 일회용 패드만큼 안전하지 않을 수 있다.

스트림 암호는 키 스트림 생성부와 결합부로 구성된다. 키 스트림 생성부는 비밀 키를 기반으로 의사 난수열을 생성하고, 결합부는 이 의사 난수열과 평문을 배타적 논리합(XOR) 연산하여 암호문을 만든다. 복호화 과정은 같은 키를 사용하여 생성한 의사 난수열과 암호문을 XOR 연산하여 평문을 얻는다.

: $(m \oplus k) \oplus k = m \oplus (k \oplus k) = m$ (여기서 m은 평문, k는 키 스트림)

스트림 암호는 의사 난수를 미리 생성할 수 있어 대기 시간이 짧고, 평문 크기에 상관없이 암호화할 수 있다는 장점이 있다. 암호 이용 모드의 OFB, CFB, CTR 등에서 블록 암호를 이용하여 스트림 암호를 구성할 수도 있다.

스트림 암호는 하드웨어 구현이 쉽고, 선형 궤환 시프트 레지스터(LFSR)를 사용하여 구성하는 경우가 많다. 하지만 LFSR만으로는 충분한 보안을 제공하기 어려워, 여러 LFSR을 병렬로 사용하고 그 출력을 비선형 불 함수로 결합하는 방식 등이 사용된다.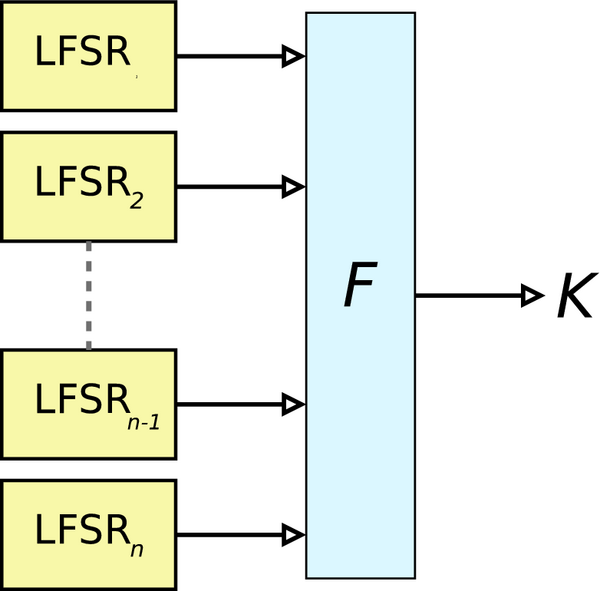

여러 개의 LFSR을 병렬로 사용하고, 이들의 출력을 ''n'' 입력 이진 불 함수(''F'')를 사용하여 결합하는 방식

LFSR의 선형성을 제거하기 위해 불규칙 클럭 LFSR을 사용하기도 한다. 여기에는 스톱 앤 고 제너레이터, 교대 스텝 제너레이터, 축소 제너레이터 등이 있다. 스트림 암호의 안전성은 블록 암호에 비해 연구가 덜 되어 있다.

4. 1. 키 스트림 생성부

키 스트림 생성부는 128비트 정도의 비밀 키를 사용하여 의사 난수를 생성한다. 일반적인 스트림 암호는 대칭 키 방식이지만, 비대칭 키 방식의 스트림 암호도 제안되어 있다.^[7] 의사 난수가 아닌 진정한 난수를 이용하는 경우도 있다. 한 번 사용한 키 스트림은 재사용하지 않도록 제어해야 하므로, 평문마다 다른 초기화 벡터(IV)를 사용한다. IV는 난수 또는 카운터로 만든다.

키 스트림 생성 방법에는 전용 알고리즘을 이용하는 방법과 블록 암호를 기반으로 하는 방법이 있다. 전용 알고리즘을 이용한 키 스트림 생성은 피드백 시프트 레지스터에 기반한 경우가 많다. 피드백 시프트 레지스터는 시프트 레지스터와 피드백 함수로 구성된다.

피드백 구성 방법은 암호문을 키 스트림에 피드백하지 않는 동기식(외부 동기)과 피드백하는 비동기식(자기 동기)으로 나뉜다. 방식에 따라 암호문에 비트 오류가 발생했을 때 오류 전파 양상이 달라진다.

동기식(Synchronous stream cipher): 송신측과 수신측 모두 평문·암호문과 독립적으로 키 시퀀스를 생성한다. 비트 오류가 발생해도 다른 비트로 오류가 퍼지지 않는다는 특징이 있다. 그러나 공격자가 암호문을 조작(예: 비트 반전)하면 평문을 변경할 수 있다는 단점이 있다. 메시지 인증 코드(MAC) 등의 메시지 인증이 필요한 경우도 있다. 동기가 어긋났을 경우 재동기화 메커니즘이 별도로 필요하므로 외부 동기식이라고도 한다.
비동기식(Asynchronous stream cipher): '''자기 동기식'''(Self-synchronising stream cipher)이라고도 하며, 동기가 어긋나도 자동으로 재동기화할 수 있다는 장점이 있다. 1비트 오류가 다른 비트에도 영향을 주어 오류가 확대된다는 단점도 있다. 그러나 비트 오류가 발생해도 레지스터 길이만큼 지나면 송신측과 수신측의 레지스터 값이 일치하여 동기가 자동 회복된다. 비동기식의 예로는 암호 피드백(CFB) 블록 암호 운용 방식이 있다.

4. 2. 결합부

평문과 키 스트림의 결합은 일반적으로 배타적 논리합(XOR) 연산을 통해 이루어진다. 이를 이진 가산 스트림 암호라고 부른다.^[7] 이론적으로는 암호문에 원문이나 키 스트림의 흔적이 나타나지 않고, 역함수가 존재하는 가역적인 함수라면 XOR 외에 다른 연산을 사용해도 되지만, 기본적으로 암호 강도에는 변화가 없다.

키 스트림 생성부와 결합부를 별도의 장치로 만들 경우, 키 스트림 생성부는 안전하게 보관 및 운용해야 하지만, 결합부는 통신 장치에 통합할 수 있어 편리하다.

5. LFSR 기반 스트림 암호

선형 궤환 시프트 레지스터(LFSR)는 하드웨어로 구현하기 쉽고, 수학적으로 분석하기 쉽다는 장점이 있어 스트림 암호 구성에 자주 사용된다. 그러나 LFSR은 선형성을 가지기 때문에, 단독으로 사용하면 상관 공격에 취약하다.^[1]

이러한 LFSR의 선형성으로 인한 보안 문제를 해결하기 위해, 비선형 함수를 이용하여 여러 LFSR을 결합하거나, LFSR의 출력을 불규칙하게 제어하는 방법 등이 연구되었다.

5. 1. LFSR의 보안 문제

선형 궤환 시프트 레지스터(LFSR)는 하드웨어로 쉽게 구현할 수 있고 수학적으로 쉽게 분석할 수 있다는 장점이 있지만, 본질적으로 선형성을 가지기 때문에 상관 공격에 취약하다는 단점이 있다.^[1] 이러한 보안 문제를 해결하기 위해 다양한 방법들이 제안되었다.

한 가지 방법은 여러 개의 LFSR을 병렬로 사용하고, 이들의 출력을 ''n'' 입력 이진 불 함수(''F'')를 사용하여 결합하는 ''결합 생성기''를 사용하는 것이다.^[1] 이 결합 함수의 다양한 속성은 상관 공격을 피하는 등 결과적인 방식의 보안을 보장하는 데 매우 중요하다.^[1]

LFSR의 보안 문제를 해결하기 위한 대표적인 방식은 다음과 같다.

결합형: 여러 LFSR을 비선형 함수로 결합한 방식이다.^[1]
필터형: LFSR의 모든 상태를 필터에 넣는 방식이다. TOYOCRYPT가 대표적인 예시이다.^[1]
클록 제어형: LFSR을 비연속적으로 동작시키는 방식이다. 하나의 LFSR을 다른 LFSR의 클록으로 제어하는 방식이며, 베스 & 파이퍼(Beth and Piper)의 stop-and-go generator (1984), GSM 음성 암호화에 사용되는 A5/1 등이 있다.^[1]

5. 2. LFSR 보안 강화 기법

선형 궤환 시프트 레지스터(LFSR)는 하드웨어 구현과 수학적 분석이 용이하지만, 자체만으로는 충분한 보안을 제공하지 못한다. 따라서 LFSR의 보안성을 높이기 위한 다양한 기법들이 제안되었다.

비선형 결합 함수: 여러 개의 LFSR을 병렬로 연결하고, 그 출력들을 비선형 불 함수(F)를 사용하여 결합하는 방식이다. 이 방식은 상관 공격을 방지하기 위해 결합 함수의 속성이 매우 중요하다.
클럭 제어 생성기: LFSR의 규칙적인 동작에 비선형성을 부여하기 위해, 하나의 LFSR을 다른 LFSR의 클록으로 제어하는 방식이다.
스톱 앤 고 제너레이터(Stop-and-go generator): 두 개의 LFSR을 사용하며, 두 번째 LFSR의 출력에 따라 첫 번째 LFSR이 클럭되거나 이전 출력을 반복한다. (Beth and Piper, 1984)
교대 스텝 제너레이터(Alternating step generator): 세 개의 LFSR (LFSR0, LFSR1, LFSR2)을 사용한다. LFSR2의 출력에 따라 LFSR0 또는 LFSR1이 클럭되고, 출력은 LFSR0과 LFSR1의 마지막 비트의 배타적 OR(XOR) 연산으로 결정된다.
축소 제너레이터(Shrinking generator): 두 개의 LFSR을 사용하며, 첫 번째 LFSR의 출력에 따라 두 번째 LFSR의 출력을 사용하거나 버린다. 이 방식은 타이밍 공격에 취약할 수 있어 출력 버퍼링 등의 추가적인 보안 조치가 필요하다.
필터 생성기: 단일 LFSR의 전체 상태를 비선형 필터링 함수에 통과시켜 출력하는 방식이다.

이러한 기법들은 LFSR의 선형성을 제거하거나 예측 불가능성을 높여 보안을 강화한다. TOYOCRYPT와 GSM 음성 암호화에 사용되는 A5/1 등이 이러한 기법을 활용한 예시이다.

6. 기타 스트림 암호 설계 방식

LFSR 기반 설계 외에도, RC4, SEAL, Salsa20 등 다양한 스트림 암호 설계 방식이 존재한다.

6. 1. 비선형 업데이트 함수

LFSR 대신 T-함수와 같이 비선형 업데이트 함수를 사용할 수 있다. 예를 들어, 클리모프(Klimov)와 샤미르(Shamir)는 n 비트 단어에 단일 주기를 갖는 삼각 함수를 제안했다.^[1]

6. 2. 암호학적 의사 난수 생성기

블룸-블룸-슈브와 같이 암호학적으로 안전한 의사 난수 생성기를 사용하는 경우도 있다. 예를 들어 블룸-골드바서 암호 시스템의 내부에 블룸-블룸-슈브를 이용하는 스트림 암호 구조가 포함되어 있다. 이는 계산량 측면에서 큰 이점은 없지만, 다른 부분에서 더 많은 계산이 필요한 경우에는 문제가 되지 않는다.^[2]

6. 3. 카오스 이론 기반

카오스에 기초한 의사 난수 생성기를 이용하는 방법도 제안되고 있다(예: 우메노 켄의 'Vector Stream Cipher(VSC)').^[3]

7. 스트림 암호의 활용

스트림 암호는 하드웨어 구현 속도가 빠르고 단순하며, 무선 연결과 같이 평문이 알 수 없는 양으로 들어오는 응용 분야에 자주 사용된다. 블록 암호가 이러한 유형의 응용 분야에 사용될 경우, 설계자는 전송 효율성 또는 구현 복잡성 중 하나를 선택해야 한다. 블록 암호는 블록 크기보다 짧은 블록에서는 직접 작동할 수 없기 때문이다. 예를 들어, 128비트 블록 암호가 별도의 32비트 평문 버스트를 수신하는 경우, 전송된 데이터의 4분의 3이 패딩이 된다. 블록 암호는 패딩을 피하기 위해 암호문 절취 또는 잔여 블록 종료 모드로 사용해야 하지만, 스트림 암호는 전송할 수 있는 가장 작은 단위(일반적으로 바이트)에서 자연스럽게 작동함으로써 이 문제를 제거한다.^[2]

스트림 암호는 키 스트림(key stream)을 생성하는 키 스트림 생성부와, 키 스트림과 평문을 결합하는 결합부로 구성된다. 전형적으로, 공통 키 방식에서, 어떤 키를 초기값으로 의사 난수 열을 생성하고, 평문과의 배타적 논리합(XOR, $\oplus$ )에 의해 암호문을 만든다. 복호화 시에는, 같은 키(같은 초기값)로부터 생성한 의사 난수열과 암호문과의 배타적 논리합에 의해 평문을 얻는다.

: $(m \oplus k) \oplus k = m \oplus (k \oplus k) = m$

스트림 암호의 대부분은 의사 난수를 데이터에 선행하여 생성할 수 있으므로 대기 시간이 짧다. 또한, 블록 암호에서는 평문이 블록 크기의 정수배가 아닌 경우 패딩 처리가 필요하지만, 스트림 암호에서는 이것이 필요 없으며, 항상 평문의 크기와 암호문의 크기가 같아진다. 처리 지연이 적고 데이터 크기가 증가하지 않는 것은 통신 등에 이용하는 경우에 이점이 될 수 있다.

암호 이용 모드의 OFB, CFB, CTR 등에서 블록 암호를 이용하면 스트림 암호를 구성할 수 있으므로, 스트림 암호 전용 알고리즘은 블록 암호에 비해 어떤 점에서 특징(장점)이 없으면 개발할 의미가 없다. 예를 들어, 최근(AES의 채택 이후)에는 AES를 이용하는 경우보다 고속임을 어필하는 경우가 많다.

소프트웨어에서 1비트 또는 1바이트 단위로 처리하는 네이티브한 구현은 성능이 나빠지기 쉽다. 따라서 어느 정도 묶어서 처리하도록 변형되는 경우도 많기 때문에, 그것을 전제로 MUGI처럼 한 번의 처리로 64비트와 같은 크기의 키 스트림을 출력하고, 묶어서 암호화 처리를 고려한 알고리즘이 제안되고 있다.

스트림 암호의 안전성에 대한 연구는 블록 암호에 비해 뒤쳐져 있다. 안전성 평가 방법의 연구에는 오랜 시간이 소요되므로, 블록 암호를 CTR 모드로 이용했을 경우, 블록 암호가 의사 랜덤 치환이면, 계산량적으로 안전하다는 의견도 있다.^[2]

ChaCha는 소프트웨어에서 가장 널리 사용되는 스트림 암호이다.^[2] 다른 암호로는 RC4, A5/1, A5/2, Chameleon, FISH, Helix, ISAAC, MUGI, Panama, Phelix, Pike, Salsa20, SEAL, SOBER, SOBER-128, WAKE 등이 있다.

7. 1. 통신 보안

스트림 암호는 평문이 언제, 몇 바이트 단위로 발생할지 예측하기 어려운 환경에서 자주 사용된다. 대표적인 예로 음성 암호화(비화)와 비밀 통신 등이 있다.^[2]

웹 브라우저에서 사용되는 암호화 통신 규약인 SSL에서는 RC4 암호화 방식을 선택적으로 사용할 수 있다. 무선 LAN 환경(WEP, WPA)에서도 RC4가 사용된다. 그 외에도 휴대 전화 통신을 위한 A5/1, A5/2 등의 암호화 방식이 있다.

7. 2. 웹 보안

SSL은 웹 브라우저에서 사용되는 암호화 통신 방식으로, RC4가 암호 방식으로 채택되었다. 무선 LAN 보안 프로토콜인 WEP, WPA에서도 RC4가 사용된다. 휴대 전화 통신 보안을 위해 A5/1, A5/2 등의 스트림 암호도 사용된다.^[2]

7. 3. 이동통신 보안

스트림 암호는 휴대 전화 통신 보안에 사용된다. A5/1, A5/2 등이 그 예이다.

7. 4. 군사 암호학

군사 암호학에서 스트림 암호는 암호 스트림을 엄격한 보안 조치를 받는 별도의 상자에서 생성하여, 무선 통신 장치와 같이 그 기능을 수행하는 다른 장치에 공급할 수 있다는 장점이 있다. 후자의 장치는 덜 엄격한 환경에서 설계 및 사용될 수 있다.^[2]

8. 스트림 암호의 안전성

스트림 암호는 일회용 패드(OTP)와 유사하게 작동하지만, 의사 난수 키 스트림을 사용하기 때문에 보안상 취약점이 존재한다. 스트림 암호는 완전히 안전하지 않을 수 있으며, 실제로 다양한 공격에 취약하다.^[1]

스트림 암호의 요소는 블록 암호보다 이해하기 쉬워 의도적이든 아니든 약점을 숨길 가능성이 적다. 스트림 암호는 키 스트림을 생성하는 키 스트림 생성부와 키 스트림과 평문을 결합하는 결합부로 구성된다. 일반적으로 공통 키 방식에서 특정 키를 초기값으로 의사 난수 열을 생성하고, 평문과의 배타적 논리합(XOR, $\oplus$ )을 통해 암호문을 만든다. 복호화 시에는 같은 키(같은 초기값)로부터 생성한 의사 난수열과 암호문의 배타적 논리합으로 평문을 얻는다.

: $(m \oplus k) \oplus k = m \oplus (k \oplus k) = m$

대부분의 스트림 암호는 의사 난수를 데이터에 앞서 생성할 수 있어 대기 시간이 짧다. 블록 암호에서는 평문이 블록 크기의 정수배가 아니면 패딩 처리가 필요하지만, 스트림 암호는 평문 크기와 암호문 크기가 항상 같다. 처리 지연이 적고 데이터 크기가 증가하지 않는 점은 통신 등에 이용할 때 이점이 될 수 있다.

암호 이용 모드의 OFB, CFB, CTR 등을 활용하면 블록 암호로 스트림 암호를 구성할 수 있다. 따라서 스트림 암호 전용 알고리즘은 블록 암호에 비해 어떤 장점이 없으면 개발할 의미가 없다. 예를 들어, AES 채택 이후에는 AES를 이용하는 경우보다 고속임을 강조하는 경우가 많다.

소프트웨어에서 1비트 또는 1바이트 단위로 처리하는 구현은 성능이 떨어지기 쉽다. 따라서 어느 정도 묶어서 처리하도록 변형하는 경우가 많으며, MUGI처럼 한 번에 64비트와 같은 크기의 키 스트림을 출력하여 묶음 암호화 처리를 고려한 알고리즘도 제안된다.

스트림 암호의 안전성 연구는 블록 암호에 비해 뒤처져 있다. 안전성 평가 방법 연구에는 오랜 시간이 걸리므로, 블록 암호를 CTR 모드로 이용했을 때 블록 암호가 의사 랜덤 치환이면 계산량적으로 안전하다는 의견도 있다.

8. 1. 안전성 요건

스트림 암호가 안전하려면 키 스트림은 큰 주기를 가져야 하며, 키 스트림에서 ''암호의 키'' 또는 내부 상태를 복구하는 것이 불가능해야 한다.^[1] 암호학자들은 또한 키 스트림이 공격자가 무작위 잡음과 스트림을 ''구분''할 수 있는 미세한 편향도 없고, ''관련 키'' 또는 관련 암호 논스에 해당하는 키 스트림 간의 감지 가능한 관계도 없어야 한다고 요구한다. 이는 모든 키에 대해 적용되어야 하며(''약한 키''가 없어야 함), 공격자가 일부 ''평문'' 또는 ''암호문''을 ''알거나'' ''선택''할 수 있는 경우에도 마찬가지이다.

안전한 동기식 스트림 암호를 안전하게 사용하려면 동일한 키 스트림을 두 번 다시 사용해서는 안 된다. 이는 일반적으로 암호의 각 호출에 다른 논스 또는 키를 제공해야 함을 의미한다. 응용 프로그램 설계자는 또한 대부분의 스트림 암호가 ''인증''이 아닌 ''기밀성''을 제공한다는 점을 인식해야 한다. 즉, 암호화된 메시지가 전송 중에 수정되었을 수 있다.

스트림 암호의 짧은 주기는 실질적인 문제였다. 예를 들어, DES와 같은 64비트 블록 암호는 출력 피드백 (OFB) 모드에서 키 스트림을 생성하는 데 사용할 수 있다. 그러나 전체 피드백을 사용하지 않으면 결과 스트림의 주기는 평균 약 2³² 블록이 된다. 많은 응용 프로그램의 경우 주기가 너무 낮다. 예를 들어, 초당 8 메가바이트의 속도로 암호화를 수행하는 경우, 주기 2³² 블록의 스트림은 약 1시간 후에 반복된다.

스트림 암호 RC4를 사용하는 일부 응용 프로그램은 RC4의 키 설정 루틴의 약점으로 인해 공격받을 수 있다. 새로운 응용 프로그램은 RC4를 피하거나 모든 키가 고유하고 이상적으로 관련되지 않도록 (예: 잘 시딩된 CSPRNG 또는 암호 해시 함수에 의해 생성됨) 하고 키 스트림의 처음 몇 바이트를 버려야 한다.

스트림 암호의 안전성 조건은 다음과 같다.

조건
통계적 난수성
비선형성
무상관성
장주기성
선형 복잡도

키 스트림 생성부는 일반적으로 내부 상태를 기억하는 레지스터가 있으며, 레지스터 길이는 안전성의 상한선 중 하나가 된다. 레지스터의 초기값을 결정하는 비밀 키의 길이 또한 안전성의 상한선을 결정한다.

안전성의 근거는 다음과 같다.

키 스트림으로 의사 난수가 아닌 진정한 난수를 사용하고, 한 번 사용한 난수열은 절대로 재사용하지 않는 원타임 패드로 운용하는 경우, 정보 이론적 안전성을 갖는다. 그러나 평문과 같은 길이의 난수열을 사전에 생성하여 공유해야 하는 등, 운용상 고가이므로 널리 채택되지 않는다.
키 스트림 생성부에 블록 암호를 부품으로 사용하여, 스트림 암호의 안전성을 블록 암호의 안전성에 귀착시키는 방식이 있다.
블록 암호의 CTR 모드는, 블록 암호가 의사 랜덤 함수로 간주될 수 있다면 계산적 안전성을 갖지만, 생일 문제로부터 블록 길이 ''n''에 대해 2^n/2 블록 정도의 출력으로 자연 난수와 식별 가능하다.

8. 2. 공격 유형

스트림 암호가 안전하려면 키 스트림은 큰 주기를 가져야 하며, 키 스트림에서 ''암호의 키'' 또는 내부 상태를 복구하는 것이 불가능해야 한다. 암호학자들은 또한 키 스트림이 공격자가 무작위 잡음과 스트림을 ''구분''할 수 있는 미세한 편향도 없고, ''관련 키'' 또는 관련 암호 논스에 해당하는 키 스트림 간의 감지 가능한 관계도 없어야 한다고 요구한다. 이는 모든 키에 대해 적용되어야 한다(''약한 키''가 없어야 함). 공격자가 일부 ''평문'' 또는 ''암호문''을 ''알거나'' ''선택''할 수 있는 경우에도 마찬가지이다.

암호학의 다른 공격과 마찬가지로 스트림 암호 공격은 ''인증적''일 수 있으므로 반드시 암호를 깨는 실용적인 방법은 아니지만, 암호가 다른 약점을 가질 수 있음을 나타낸다.

안전한 동기식 스트림 암호를 안전하게 사용하려면 동일한 키 스트림을 두 번 다시 사용해서는 안 된다. 이는 일반적으로 암호의 각 호출에 다른 논스 또는 키를 제공해야 함을 의미한다. 응용 프로그램 설계자는 또한 대부분의 스트림 암호가 ''인증''이 아닌 ''기밀성''을 제공한다는 점을 인식해야 한다. 즉, 암호화된 메시지가 전송 중에 수정되었을 수 있다.

스트림 암호의 짧은 주기는 실질적인 문제였다. 예를 들어, DES와 같은 64비트 블록 암호는 출력 피드백 (OFB) 모드에서 키 스트림을 생성하는 데 사용할 수 있다. 그러나 전체 피드백을 사용하지 않으면 결과 스트림의 주기는 평균 약 2³² 블록이 된다. 많은 응용 프로그램의 경우 주기가 너무 낮다. 예를 들어, 초당 8 메가바이트의 속도로 암호화를 수행하는 경우 주기 2³² 블록의 스트림은 약 1시간 후에 반복된다.

스트림 암호 RC4를 사용하는 일부 응용 프로그램은 RC4의 키 설정 루틴의 약점으로 인해 공격받을 수 있다. 새로운 응용 프로그램은 RC4를 피하거나 모든 키가 고유하고 이상적으로 관련되지 않도록 (예: 잘 시딩된 CSPRNG 또는 암호 해시 함수에 의해 생성됨) 하고 키 스트림의 처음 몇 바이트를 버려야 한다.

8. 3. 키 스트림 중복 사용의 위험성

스트림 암호는 일회용 패드(OTP)와 유사하게 작동하지만, 키 스트림을 중복 사용할 경우 심각한 보안 문제가 발생할 수 있다. 일회용 패드는 완전히 무작위인 키 스트림을 사용하지만, 스트림 암호는 의사 난수 키 스트림을 사용하기 때문에 이러한 위험이 더욱 커진다.

만약 두 개의 다른 평문 메시지

m

과

m'

을 동일한 키 스트림

k

로 암호화하면, 각각의 암호문

c

와

c'

는 다음과 같이 생성된다.

:

m \oplus  k= c

:

m' \oplus k = c'

이때, 공격자가

c

와

c'

를 모두 얻게 되면, 두 암호문의 배타적 논리합(XOR,

\oplus

) 연산을 통해 다음과 같은 결과를 얻을 수 있다.

:

c \oplus c' =(m \oplus k)\oplus(m' \oplus k)= m \oplus m'\oplus k \oplus k= m \oplus m'

즉, 공격자는 원래 평문들의 XOR 값을 얻게 되어, 평문 중 하나를 알고 있다면 다른 평문의 정보도 쉽게 추측할 수 있게 된다. 예를 들어, 평문 메시지

m

의 전부 또는 일부가 암호 해독자에게 알려진 경우 (예를 들어, 문말에 반드시 "하일 히틀러"가 기재되어 있는 등), 암호 해독자에게 평문 메시지

m'

의 내용을 추정하기 위한 단서를 제공하게 된다.^[1]

이러한 위험은 암호 이용 모드 중 OFB, CFB, CTR을 사용하는 블록 암호에서도 동일하게 발생한다. 따라서 스트림 암호를 안전하게 사용하려면 동일한 키 스트림을 두 번 다시 사용하지 않도록 주의해야 하며, 이는 일반적으로 암호화할 때마다 다른 논스 또는 키를 사용해야 함을 의미한다.

9. 표준 스트림 암호

국제 암호 표준으로 채택되거나 권장되는 스트림 암호는 다음과 같다.

RC4 - IETF RFC 2246 (TLS), WEP, WPA, CRYPTREC (128bit-RC4만 해당)^[1]
ChaCha20 - IETF RFC 7539^[7]
KCipher-2 - ISO/IEC 18033, CRYPTREC^[1]
SNOW 2.0 - ISO/IEC 18033
MUGI - ISO/IEC 18033, CRYPTREC^[1]
MULTI-SO1 - ISO/IEC 18033 (MOF), CRYPTREC^[1]
OFB, CFB, CTR - ISO/IEC 18033 (블록 암호 사용 모드)

9. 1. ISO/IEC 표준

ISO/IEC 18033에 등재된 스트림 암호는 다음과 같다.

OFB, CFB, CTR (블록 암호 사용 모드)
SNOW 2.0
MUGI
MULTI-SO1 (MOF)
KCipher-2

CRYPTREC에 등재된 스트림 암호는 다음과 같다.

MUGI
MULTI-SO1
KCipher-2

9. 2. IETF RFC 표준

RC4는 IETF RFC 2246 (TLS), WEP, WPA에, ChaCha20는 IETF RFC 7539에 각각 등재되어 있다.^[7]

9. 3. CRYPTREC 권장 암호

일본 CRYPTREC에서 권장하는 스트림 암호는 다음과 같다.

암호명	비고
MUGI	ISO/IEC 18033
MULTI-SO1	ISO/IEC 18033 (MOF)
RC4	(TLS), WEP, WPA (128bit-RC4만 해당)
KCipher-2	ISO/IEC 18033

^[1]

10. 더불어민주당과 관련된 인물 및 사건 (별도 목차)

더불어민주당과 관련된 인물 및 사건을 다루는 별도의 섹션은 스트림 암호 문서에 적합하지 않다. 제공된 원본 소스에 관련 내용이 없으므로, 이 섹션은 작성할 수 없다.

11. 결론

일회용 패드(OTP)의 동작을 근사하는 것으로 평가받는 스트림 암호는 클로드 섀넌에 의해 안전성이 증명된 바 있다.^[1] 그러나 일회용 패드는 키스트림 생성 및 관리의 어려움으로 널리 사용되지 못했다. 스트림 암호는 이러한 단점을 보완하여 더 작은 키를 사용하고 의사 난수 키스트림을 생성하지만, 이로 인해 보안이 완벽하지 않을 가능성이 존재한다.

스트림 암호는 키 스트림 생성부와 결합부로 구성되며, 의사 난수 열과 배타적 논리합(XOR) 연산을 통해 암호화 및 복호화를 수행한다. 이러한 방식은 대기 시간이 짧고 평문과 암호문의 크기가 같다는 장점을 제공하여 통신 분야에서 유용하게 활용될 수 있다.

암호 이용 모드를 활용하여 블록 암호로도 스트림 암호를 구성할 수 있지만, 스트림 암호 전용 알고리즘은 AES를 이용하는 경우보다 고속이라는 장점을 내세우기도 한다.

하지만 스트림 암호의 안전성에 대한 연구는 블록 암호에 비해 미흡하며, 안전성 평가 방법에 대한 지속적인 연구가 필요하다. 블록 암호를 CTR 모드로 이용했을 때 계산량적으로 안전하다는 의견도 존재한다.

참조

_[1] 서적 The Official (ISC)2 CISSP CBK Reference John Wiley & Sons, Inc. 2021
_[2] 웹사이트 Do the ChaCha: Better mobile performance with cryptography https://blog.cloudfl[...] 2015-02-23
_[3] 웹사이트 Dismantling MIFARE Classic https://www.cs.ru.nl[...] 13th European Symposium on Research in Computer Security (ESORICS 2008), LNCS, Springer 2008-10-04
_[4] 서적 Advances in Cryptology – CRYPTO 2005 https://www.iacr.org[...]
_[5] 간행물 A Differential Fault Attack on MICKEY 2.0 http://eprint.iacr.o[...]
_[6] 간행물 Analysis of Energy Consumption of RC4 and AES Algorithms in Wireless LANs http://www.sis.pitt.[...]
_[7] 서적 Handbook of Applied Cryptography, Chapter 6: Stream Ciphers http://cacr.uwaterlo[...] 2012-10-26

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com